Theorie ...

... und Praxis.

Den Ausgangspunkt bildet ein relativ klar umrissenes Lernstoffgebiet.

Zum Beispiel: Dreiecke

Dieses zerlegt man in kleine Stoffeinheiten oder nach Begriffen oder Definitionen. Diese nennen wir Wissensbausteine. (in der Literatur meist mit skills bezeichnet).

In diesem Falle soll vereinfacht folgendes genügen:

• Begriff des Dreiecks (B)
• Rechtwinklige Dreiecke (R)
• Gleichseitige Dreiecke (G)
• Satz des Phytagoras (P)

Diese bauen mit der Vorwissens-Relation aufeinander auf, d.h. ein Baustein kann notwendiges Vorwissen für einen anderen sein.

z.B. ist Begriff des  Dreiecks ein Vorwissen für gleichseitige Dreiecke, ebenso kann man den Satz des Phytagoras erst verstehen, wenn man weiß, was ein Rechtwinkliges Dreieck ist.

Diese Relation ist transitiv, d.h. Wenn A Vorwissen von B ist und B Vorwissen von C, dann ist A auch Vorwissen von C.

z. B.

• der Satz des Phytagoras hat als Vorwissen Rechtwinklige Dreiecke

• Rechtwinklige Dreiecke hat als Vorwissen die Begriff des  Dreiecks

• Sicher ist Begriff des  Dreiecks auch notwendiges Vorwissen für den Satz des Phytagoras 

In der Regel steht aber nicht jeder Wissensbaustein mit jedem anderen in dieser Vorwissensrelation.

z.B. kann man bei Rechtwinkliges Dreieck und Gleichseitiges Dreieck nicht sagen, dass eines notwendiges Vorwissen für das andere ist.

Ein Baustein kann auch mehrere Bausteine als Vorwissen haben, bzw. Vorwissen für mehrere Bausteine sein.

Begriff Dreieck ist z. B. Vorwissen für alle anderen Bausteine

Über die Vorwissensrelation lassen sich die Bausteine in einem Diagramm anordnen. Eine aufsteigende Linie zwischen zwei Bausteinen bedeutet, dass der untere Baustein Vorwissen für den oberen ist. Es werden aber nicht alle Beziehungen eingezeichnet: Gibt es zwischen zwei Bausteinen einen „aufsteigenden Pfad“ solcher Verbindungen, so ist der untere Baustein Vorwissen für den oberen. Dies entspricht der oben erwähnten Transitivität. 

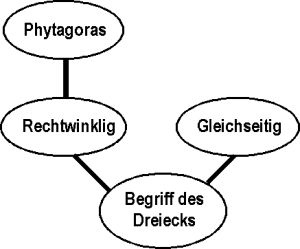
Die Menge der Bausteine mit ihrer Vorwissensrelation nennt man Wissenstruktur.

Bei TEE werden die Bausteine in dieser Wissensstruktur angeordnet und man kann in diesem Diagramm navigieren,

Das ist das Diagramm, was man bei TEE oben links in der Ecke sieht. Die den Wissensbausteinen zugeordnete Aufgaben prüfen, ob der Schüler dieses Wissen besitz.

Zusatz: Um solche Strukturen von Experten zu erfragen, verwendet man meist die Umkehrung der Vorwissensrelation, nämlich die Vermutungsrelation (surmise relation): Wenn der Schüler das Wissen B hat, besitz er vermutlich auch Wissen A. (entspricht A ist Vorwissen von B).

Wenn jemand den Satz des Phytagoras verstanden hat, sollte er auch wissen, was ein rechtwinkliges Dreieck ist

Der Wissensraum (knowledge space)

Der Schüler beherrscht eine gewisse Anzahl von Wissenbausteinen. Diese Menge bezeichnet man als Wissensstand oder Wissenszustand. 

z.B. kennt er den Begriff des Dreiecks, Rechtwinklige Dreiecke und Gleichseitige Dreiecke, kurz geschrieben als

{B, R, G}

Dabei ist aufgrund der Wissensstruktur nicht jede beliebige Menge von Wissensbausteinen ein Wissenszustand, sondern in zu jedem Wissensbaustein einen Wissensstandes muss auch das gesamte Vorwissen mit im Wissensstand enthalten sein.
Man setzt also voraus, das der Schüler nichts vergisst.

z.B. ist {R, G} kein Wissenstand: Wenn der Schüler Rechtwinklige Dreiecke und gleichseitige Dreiecke kennt, müsste er auch den Begriff des Dreiecks kennen.

Mögliche Wissensstände sind hier im Beispiel:

Æ, {B}, {B, R}, {B, G}, {B, R, G}, {B, R, P}, {B, R, G, P} 

Durch Lernen kann sich der Schüler einen weiteren Wissensbaustein aneignen und gelangt so zu einem neuen Wissensstand. Auf diese Weise kann man die Wissensstände jetzt zueinander in Beziehung setzen: ein Wissensstand A ist möglicher vorheriger Wissenstand von B, wenn A eine Teilmenge von B ist, d.h. alle Wissensbausteine von A in B enthalten sind. Übertragen bedeutet dies, das der Schüler von Wissenstand A durch erwerben von Wissensbausteinen den  Wissensstand B  erreichen kann.

z.B. ist

• {B, R} ein möglicher vorheriger Wissenstand von {B, R, G}

• {B, R} ist auch möglicher vorheriger Wissenstand für {B, R, G}

• {B, G} ist kein möglicher vorheriger Wissenstand von {B, R, P} (wegen G)

• Æ ist natürlich möglicher vorheriger Wissenstand für alle anderen Wissensstände

Diese Beziehung ist ebenfalls transitiv.

Das ist einleuchtend, da ja ein möglicher vorheriger Wissenstand einfach ein paar Wissensbausteinen weniger hat

Somit kann man die Wissensstände auch wieder in einem Diagramm darstellen. Gibt es von A nach B einen aufsteigenden Pfad, so ist A möglicher vorheriger Wissenstand von B.

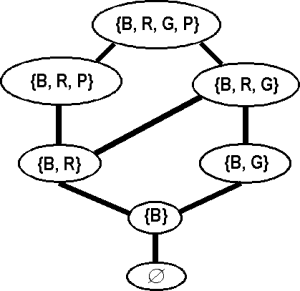
Bei TEE gibt es zu jedem Wissenstand eine (eigentlich mehrere) Färbungszustände der Wissensstruktur.

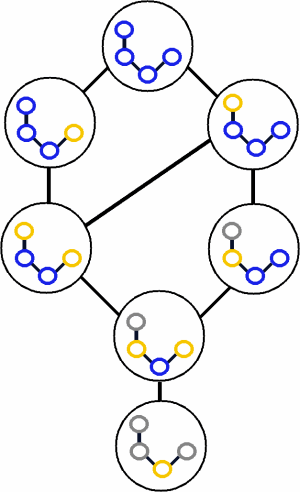
Die Wissensstände mit ihre „möglicher vorheriger Wissenstand“-Relation nennt man Wissensraum (knowledge space)

Der Wissensraum wird bei TEE nicht abgezeigt, der Lernende bewegt sich aber auf einem Pfad von unten nach oben von einem Zustand zum nächsten.

Intelligent Tutorial System (ITS)

Die Aufgabe eine intelligenten (adaptiven) Lernsystems ist es, möglichst rasch den vorhandenen Wissensstand des Schülers zu ermitteln und dann automatisch weiterführende Wissensbausteine anzubieten die dem aktuellen Wissenstand entsprechen. Zum Ermitteln des Wissensstandes wird durch Fragen und Aufgaben wird ermittelt, ob der Schüler einzelne Wissensbausteine beherrscht. Die Eigenschaften des Wissensraums werden genutzt, um die Menge der Fragen möglichst gering zu halten.

In der Regel verwendet man zum Ermitteln des Wissensstandes sogenannte Half-Split-Verfahren (Halbierungsverfahren). Zu Anfang ist jeder Wissenstand möglich. Um über einem Wissensbaustein möglichst viel Wissenszustände auszuschließen, fragt man nach einem Wissensstand aus der Mitte der Wissensstruktur. Wird dieser Baustein gemeistert, kann man alle Wissensstände ausschließen, die den Baustein nicht enthalten. Scheitert der Schüler, kann man alle Wissensstände ausschließen, die den Wissensbaustein enthalten. Für die verbleibenden möglichen Wissensständen wiederholt man den Prozess: Man wählt eine Wissensbaustein und schließt damit weitere Wissensstände aus. Das führt man so lange fort, bis nur noch ein Wissensstand übrig ist.

Das Problem dabei ist, möglichst optimale Wissensbausteinen zu wählen. Am besten ist es natürlich, wenn der Baustein in der Hälfte der Wissensstände vorkommt: je nach dem, ob der Schüler den Baustein meistert, kann man die eine oder andere Hälfte der Wissensstände ausschießen (daher „Halbierungsverfahren“).

Wird TEE im ITS-Modus verwendet, so verhält es sich wie genauso wie oben beschrieben: Zuerst wird der Wissensstand ermittelt (über Aufgaben), danach schaltet das System in den „Zufall restriktiv“ Modus und präsentiert zu lernende Wissensbausteine.
Die Wissensbausteine können dabei nicht vom Schüler ausgewählt werden.